What are Random Forests?
Random Forests are a collection of many Classification and Regression Trees (CARTs) which in turn originate from a fairly basic management tool, decision trees. Decision trees have been commonly used in various industries to crystallise outcomes and their probabilities. Many of us use decision trees subconsciously, assessing the range of possibilities against how well it match our preferred outcome.
The basics
Quantitative screens can quite easily be translated into a decision tree, for example, a simple value/quality quant screen can be represented by the following decision tree:
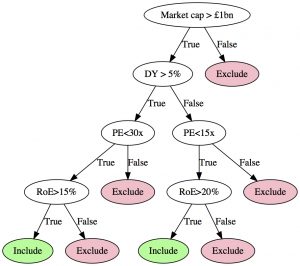
In a machine-learned classification tree, the split point and variable to use at each node is recursively determined by considering the training data, provided that all the training data has already been classified. For instance, if we would like to build a set of rules to determine whether stocks are likely to outperform or underperform in the next quarter, we can use historical quarterly returns and classify stocks based on their performance against a benchmark, using their market cap, dividend yield, PE and RoE ratios as in the example above.
The CART algorithm will determine the set of cut-off points and variables that would be able to classify the training data and if allowed to grow very deep and complex trees, the resultant classification tree would be able to perfectly map the input data to the known classification. This set of rules, which could use the same variables multiple times with different split points, could then be used to classify stocks not included in the training data set.
The problem is that very complex and deep trees are likely to overfit the training data: it might be able to perfectly classify stocks in the training data set but perform poorly or even completely fail when used on new data.
Random Forests: Providing the consensus view
Breiman (2000) introduced Random Forests as one alternative of overcoming overtraining. Instead of using the entire training data set to build one tree, Breiman argued that building many decision trees on subsets of the training data set and then taking the centre of gravity of all the trees to determine the final classification would be more robust to overtraining. In particular, he argued that randomly selecting a subset of the observations (i.e. stocks in our example) as well as randomly selecting a subset of the variables (i.e. market cap, dividend yield, PE and RoE) would provide one possible outcome of a random tree. Repeating this random selection and growing a classification tree each time, with each tree providing a classification for all the observations in its subset, the consensus view of all the trees in the forest can be determined that should be more reliable and robust than building only one tree on all the data.
A short note on cross-validation
There are many factors that could determine the success of a random forest:
- How many trees should be in the forest?
- How many variables should be included in a subset each time?
- How many observations should be included in a subset each time?
- How deep should the tree be grown?
- How many observations should be left in a leaf?
The answers could be determined using a standard machine learning method called cross-validation. In cross-validation, the best set of parameters can be determined by holding out (yet another) part of the sample and training the Random Forest using a particular set of parameters. That set of parameters that provided the best accuracy when testing on the hold out sample is then used in the final Random Forests, which is trained on all the data.
However, normal cross-validation assumes that the observations are independent. However, in financial application, the observations are rarely independent: the return of a stock in this quarter could depend on the return of the stock last quarter (negatively or positively). It is therefore important to use time-series cross-validation when determining the optimal parameters for machine learning.
